PeriodicSpline (FPScript)
Interpoliert einen Datensatz durch eine periodische Spline-Kurve und tastet diese an vorgebbaren Stellen ab.
Syntax
PeriodicSpline(DataSet, N, SamplingMode)
oder
PeriodicSpline(Amplitude, Time, N, SamplingMode)
Die Syntax der PeriodicSpline-Funktion besteht aus folgenden Teilen:
Teil |
Beschreibung |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
DataSet |
Der Datensatz mit konstantem Abtastintervall, welcher interpoliert wird. Wenn Sie eine Datenreihe angeben, wird die X-Komponente automatisch generiert. Erlaubte Datenstrukturen sind Datenreihe, Datenmatrix, Signal, Signalreihe und Signalreihe mit zweidimensionaler X-Komponente. Es sind alle numerischen Datentypen erlaubt. Bei komplexen Datentypen erfolgt eine Betragsbildung. Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste. |
||||||||||
Amplitude |
Die Y-Komponente des zu interpolierenden Signals. Wenn Sie ein Signal angeben, wird dessen Y-Komponente verwendet. Erlaubte Datenstrukturen sind Datenreihe, Datenmatrix, Signal, Signalreihe und Signalreihe mit zweidimensionaler X-Komponente. Es sind alle numerischen Datentypen erlaubt. Bei komplexen Datentypen erfolgt eine Betragsbildung. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||||||
Time |
Die X-Komponente des zu interpolierenden Signals. Wenn Sie ein Signal angeben, wird dessen Y-Komponente verwendet. Erlaubte Datenstrukturen sind Datenreihe, Datenmatrix, Signal, Signalreihe und Signalreihe mit zweidimensionaler X-Komponente. Es sind alle numerischen Datentypen erlaubt. Bei komplexen Datentypen erfolgt eine Betragsbildung. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||||||
N |
Gibt die Anzahl der Punkte insgesamt bzw. pro X-Intervall des Signals an. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle ganzzahligen Datentypen erlaubt. Der Wert muss größer gleich 0 sein. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||||||
SamplingMode |
Gibt an, wie die berechnete Spline-Kurve abgetastet werden soll und welche Randbedingungen verwendet werden. Das Argument SamplingMode kann folgende Werte haben:
...plus einer Konstante, die die Randbedingungen bestimmt.
Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
Anmerkungen
Das Ergebnis ist immer vom Datentyp 64-Bit Fließkomma.
Das Ergebnis hat die gleiche Einheit wie das Argument DataSet.
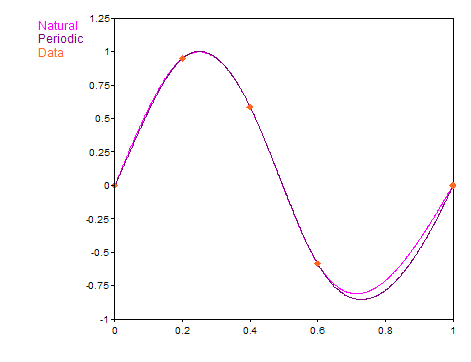
Eine Spline-Kurve besteht aus kubischen Polynomen, die so aneinander gehängt werden, dass ein möglichst glatter Verlauf entsteht. Bei der periodischen Spline-Kurve werden die Randbedingungen so festgelegt, dass die Spline-Kurve in Steigung und Krümmung am linken und rechten Rand übereinstimmt.
Der zu interpolierende Datensatz muss mindestens vier Werte enthalten und die X-Komponente muss streng monoton wachsend sein. Ist letzteres nicht der Fall (z. B. bei einer Ortskurve), so sollten Sie die ParametricSpline-Funktion verwenden. Die X-Werte müssen jedoch nicht äquidistant sein. Vor der Spline-Interpolation werden ungültige Werte in der Y-Komponente durch lineare Interpolation eliminiert.
Die folgende Grafik zeigt den Unterschied zwischen einer periodischen und einer natürlichen Spline-Kurve:
Verfügbarkeit
FlexPro Basic, Professional, Developer Suite
Beispiele
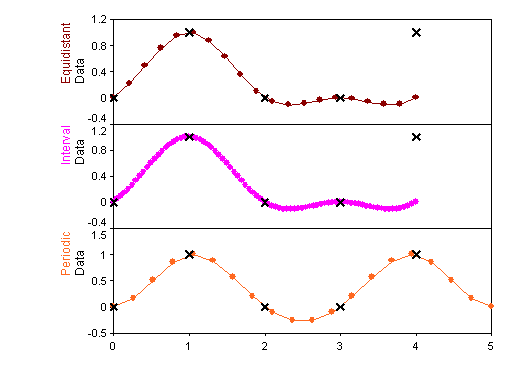
PeriodicSpline({0, 1, 0, 0, 1}, 20, SPLINE_EQUIDISTANT)
Ergibt eine äquidistant abgetastete Spline-Kurve mit 20 Werten.
PeriodicSpline({0, 1, 0, 0, 1}, 20, SPLINE_INTERVAL)
Ergibt eine Spline-Kurve mit 81 Werten.
PeriodicSpline({0, 1, 0, 0, 1}, 20, SPLINE_EQUIDISTANT+SPLINE_PERIODICAPPEND)
Ergibt eine äquidistant abgetastete periodische Spline-Kurve mit 20 Werten.
Die folgende Grafik zeigt die periodischen Spline-Kurven der drei Beispiele:
Siehe auch
Analyseobjekt Spline-Interpolation
Analyseobjekt Oberflächeninterpolation
Literatur
[1] "Carl de Boor": "A Practical Guide to Splines, Revised Edition". "Springer-Verlag, New York",2001.ISBN 0-387-95366-3.
Diese Beiträge könnten Sie ebenfalls interessieren
Sie sehen gerade einen Platzhalterinhalt von Facebook. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von Instagram. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von X. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr Informationen