weisang.com > Dokumentation > Chirp (FPScript)

FlexPro-Dokumentation

Chirp (FPScript)

21.09.2021

Berechnet einen Wobbelkosinus, d. h. ein Kosinussignal mit variabler Frequenz.

Syntax

Chirp(Time, Frequency1, Frequency2, Time2 [ , Operation = CHIRP_LINEAR ])

Die Syntax der Chirp-Funktion besteht aus folgenden Teilen:

Teil

Beschreibung

Time

Ein Datensatz mit den Zeitpunkten, für die der Wobbelkosinus berechnet werden soll.

Es sind alle Datenstrukturen erlaubt. Es sind alle numerischen Datentypen erlaubt.

Bei komplexen Datentypen erfolgt eine Betragsbildung.

Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste.

Frequency1

Ist die Frequenz, die der Wobbelkosinus bei Time = 0 haben soll.

Erlaubte Datenstrukturen sind Einzelwert. Es sind alle reellen Datentypen erlaubt.

Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt.

Frequency2

Ist die Frequenz, die der Wobbelkosinus zum Zeitpunkt Time2 haben soll.

Erlaubte Datenstrukturen sind Einzelwert. Es sind alle reellen Datentypen erlaubt.

Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt.

Time2

Ist der Zeitpunkt, zu dem der Wobbelkosinus die Frequenz Frequency2 haben soll.

Erlaubte Datenstrukturen sind Einzelwert. Es sind alle reellen Datentypen erlaubt.

Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt.

Operation

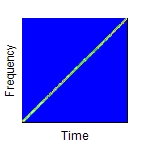
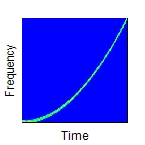
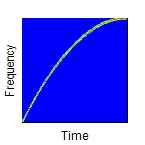
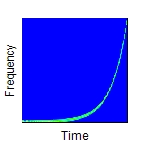
Bestimmt die Art der Frequenzvariation.

Das Argument Operation kann folgende Werte haben:

Konstante	Bedeutung
CHIRP_LINEAR	Lineare Frequenzvariation mit Momentanfrequenz: f(Time) = Frequency1 + (Frequency2 - Frequency1 ) / Time2 * Time Folgendes Spektrogramm zeigt den Verlauf der Momentanfrequenz:
CHIRP_QUADRATIC_CONCAVE	Quadratisch konkave Frequenzvariation mit Momentanfrequenz: f(Time) = Frequency1 + (Frequency2 - Frequency1 ) / Time22 * Time2 Der Scheitelpunkt der Parabel liegt hier bei Time = 0.
CHIRP_QUADRATIC_CONVEX	Quadratisch konvexe Frequenzvariation mit Momentanfrequenz: f(Time) = Frequency2 + (Frequency1 - Frequency2 ) / Time22 * (Time - Time2)2 Der Scheitelpunkt der Parabel liegt hier bei Time = Time2 .
CHIRP_EXPONENTIAL	Exponentielle Frequenzvariation mit Momentanfrequenz: f(Time) = Frequency1 + exp(log(Frequency2 - Frequency1) / Time2 * Time)

Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt.

Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert CHIRP_LINEAR gesetzt.

Anmerkungen

Der Datentyp des Ergebnisses ist immer 64-Bit Fließkomma.

Die Struktur des Ergebnisses entspricht der des Arguments Time, ggf. erfolgt die Berechnung elementweise.

Das Ergebnis hat die Einheit 1, sofern Time einheitenbehaftet ist und ansonsten keine Einheit.

Bei zusammengesetzten Datenstrukturen wird nur die Y-Komponente verrechnet und die X- und ggf. Z-Komponente wird unverändert in das Ergebnis übernommen.